2. GIS & MCDA

Slides: 2 - GIS & MCDA.pdf

---

Definition

A multi-criteria decision problem involves a set of alternatives that are evaluated on the basis of conflicting and incommensurate criteria according to the decision maker’s preferences.

Terminology

Decision maker

An entity with the responsibility to make decisions

This can be:

• Individual (e.g. searching for a house)
• Group of individuals (e.g. selecting a suitable site for housing development)
• Organization (e.g. allocating resources for housing development)

The distinction between individual and multiple decision makers are determined by the consistency of their goals, not on the number of individuals involved

Objective

A statement about the desired state of a system under consideration

We try to either maximize or minimize some attribute/function

Attributes

A property of an element of a real-world geographic system

Example: For the objective of maximizing physical accessibility to schools, the attributes such as total traveling distance, time, cost, or any other measure of spatial proximity

(Hierarchical structure)

These objectives and attributes have a hierarchical structure: we have an overarching goal, which has several objectives. These in turn are related to some attributes. All of these attributes have several potential alternatives.

Decision alternatives

Definition

Alternative courses of action among which the decision maker (agent) must choose

In the case of geographic problems, this consists of at least two elements:

• Action (what to do?)
• Location (where to do it?)

Three categories:

• Binary
• Discrete
• Continuous

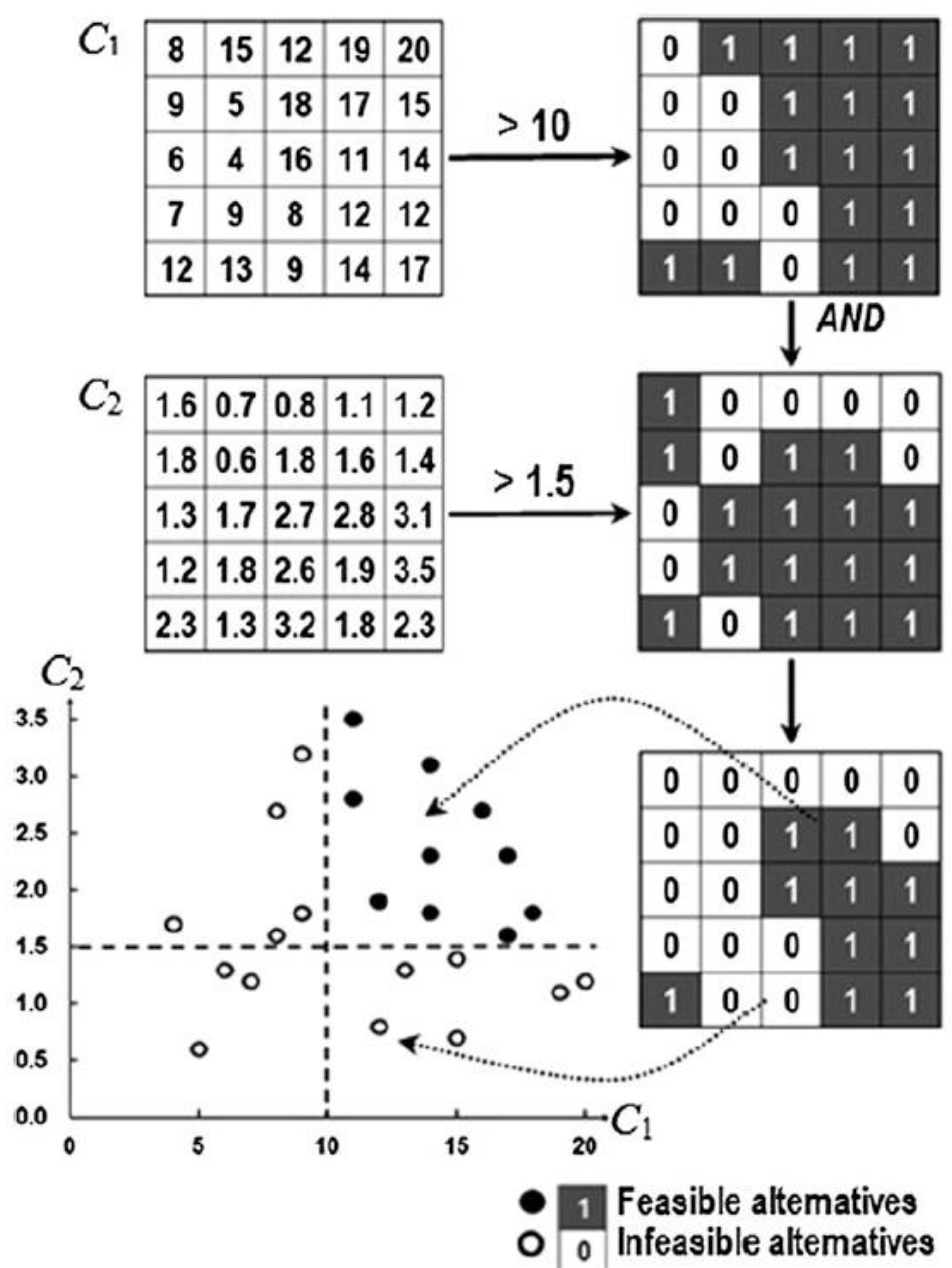
Feasible alternatives

A constraint represents restrictions imposed on decision variables. They divide alternatives into two categories:

• Acceptable (feasible)
• Unacceptable (infeasible)

These are represented in a mask-like matrix:

Value scaling

Transforms the different evaluation criteria to comparable units

The value function is a mathematical representation of human judgement

For the $k$th criterion to be maximized: $v(a_{ik})=(\frac{{\max }_i\{a_{ik}\}-a_{ik}}{r_k}{)}^{\rho }$

For the $k$th criterion to be minimized: $v(a_{ik})=(\frac{a_{ik}-{\min }_i\{a_{ik}\}}{r_k}{)}^{\rho }$

Where $r_k$ is the range, aka the max value minus the min value: $r_k={\max }_i\{a_{ik}\}-{\min }_i\{a_{ik}\}$

$\rho$ is a parameter that determines whether the value function is concave, linear, or convex.

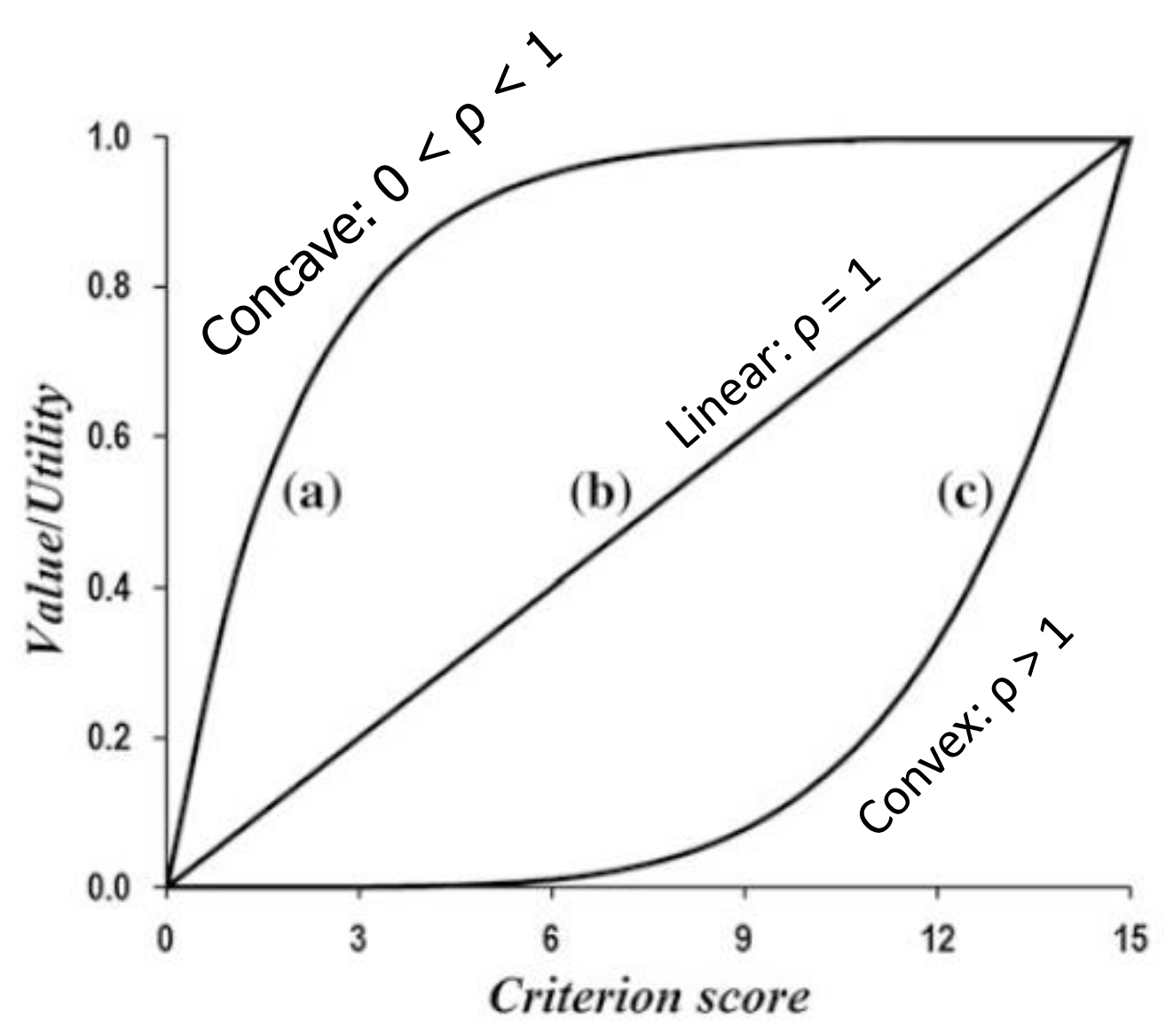
Convex: higher incremental value for additional gains, seen as risk-seeking Concave: represents diminishing returns

Examples

Convex: distance to public transport. Public transport might only become a feasible option if it’s within e.g. 10 minutes walking distance. Within that range, the closer the better, but after that it doesn’t really matter much anymore.

Concave: distance to highway. Being within a few kilometers of a highway is valuable for ease of access, but being directly adjacent may not add much benefit.

A convex function might be used for cost, where it is more important to reduce a cost from €100 to €80 than from €80 to €60.

Local value scaling

Similar to global value scaling, but a local value function represents the suitability of a particular location with respect to a specific criterion/attribute.

Example

In urban planning, the desirability of proximity to a park may vary based on existing neighborhood amenities or density, making a locally tailored assessment useful.

Criterion weighting

Definition

Weight is a value assigned to an evaluation criterion that indicates its importance relative to the other criteria under consideration.

This can be done globally (assuming spatial homogeneity of preferences), or locally if preferences differ per location

Global criteria weighting methods:

• Ranking
• Rating
• Pairwise
• Entropy-based criterion weights

We also have spatially explicit weighting methods:

Ranking method

Assign every criterion a rank (1 being most important, etc.) $w_k=\frac{n-p_k+1}{{\sum }_{i=1}^n(n-p_i+1)}$

Which can be simplified to:

$w_k=\frac{n+1-p_k}{{\sum }_{i=1}^{n}i}$

Essentially a dumber version of the rating method, that assumes the distance between all the rankings is the same

Rating method

Decision makers estimate weights on basis of predetermined scale, for example 0 to 100 (most important)

The procedure is continued until a score is assigned to the least important criterion

Finally, the weights are normalized by dividing each of the weights by the sum total

Pairwise

Instead of giving every criterion one scale, you create a matrix comparing the importance of all criteria.

	C1	C2	C3	C4	C5	weight
C1	1	1/3	1/5	1/9	1/3	0.042
C2	3	1	1	1/5	1	1.122
C3	5	1	1	1/5	3	0.180
C4	9	5	5	1	5	0.552
C5	3	1	1/3	1/5	1	0.104

Read per row: C2 is three times as important as C1

Organized into a matrix: $C=[c_{kp}{]}_{n\times n}$ Where $c_{kp}$ is the pairwise comparison for the $k$th and $p$th criteria

Normalization of Matrix C entries: $c_{kp}^{\ast }=\frac{c_{kp}}{{\sum }_{k=1}^n{c}_{kp}}\text{, for all }k=1,2,...n$

Then the weights are computed as: $w_k=\frac{{\sum }_{p=1}^n{c}_{kp}^{\ast }}{n}\text{, for all }k=1,2,...,n$

Entropy-based criterion weights

Based on the concept of information entropy

Does not require the decision making agents to specify their preferences with respect to the evaluation criteria. Instead, weights are assigned based on the variance of the criterion.

For example, if the surface areas of houses in an area are all roughly the same, the distinction holds less value.

Proximity-adjusted criterion weights

A spatially explicit method, meaning that it acknowledges the spatial heterogeneity of preferences

Combination rules

Combination rule (decision rule) integrates the data and information about alternatives (criterion maps) and decision maker’s preferences (criterion weights) into an overall assessment of the alternatives

Can be classified into four groups of:

• Compensatory versus non-compensatory
• Multiattribute versus multiobjective
• Discrete versus continues methods
• Spatially implicit versus spatially explicit MCDA

Multiattribute and Multiobjective Methods

Multicriteria decision rules can be broadly categorized into two groups:

• MultiAttribute Decision Analysis (MADA)
  • Predetermined, limited number of alternatives
  • Outcome-oriented evaluation and choice process
  • Can be seen as “discrete”
• MultiObjective Decision Analysis (MODA)
  • Process-oriented design and search
  • Make a distinction between the concept of decision variables and decision criteria
    • (Related to each other by a set of objective functions)
  • Can be seen as “continuous”

MADA: Site selection: find best site for some activity, given a set of potential sites

• Characteristics known
• Rank the best sites

MODA: Site search: no pre-determined set of candidate sites

• Characteristics such as boundary not known, goal of the analysis is to identify boundary